Professor Jason Dana and I have been experimenting with Cheating and Turker Quality on Mechanical Turk. If you haven't yet, check out Part 1. Thanks for everybody's feedback so far - please keep it coming.
Recap
When we left off, we had just offered workers on Mechanical Turk the job of flipping a coin, paying them 4 cents for a flip of heads and 2 cents for tails. We wanted to measure whether and how much particular groups of Turkers, bucketed by their quality score, would cheat when given the chance to do so.
Though our initial results seemed to suggest a positive relationship between having a high quality score and not cheating, the amount of data collected was less than desired and did not have the numbers required for statistical significance.
Experiment Two
Realizing the difficulty of attracting top Turkers to a task that offered only two cents, we decided to up the ante and make two changes: first, we renamed the task to a more attractive "One quick question. Should take ~15 seconds." Second, we raised the price of heads and tails to 10c and 5c, respectively. Once again, we asked 50 Turkers in each of our quality groups to flip a coin, for a total of 300 coin-flips.
Results
Here's what we got.
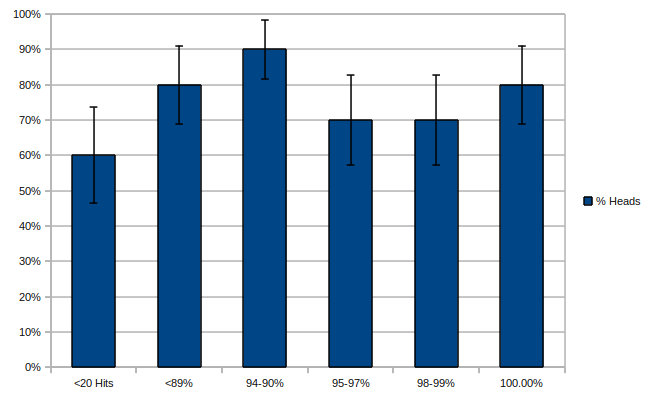
Note: Error bars are at a 95% confidence interval.
This time around, all 300 HITs (tasks) we put out were done in a matter of days. The data, however, became less clear: sure, we expected the <90% and 94-90% groups to cheat a ton (as they did), but what was the 100% group, the 'cream of the crop' doing by taking advantage of our trust and cheating as much as the lowest group, <90%?
Discussion
This bothered us for a while. Who are these 100%-ers, after all? This is the group that can do no wrong, the group that makes less than 1 error in 100. How could they have betrayed our trust, especially after we offered them more money?
Melika Cavagnaro-Wong, a friend from Wharton, provided the key insight here: 100%-ers aren't necessarily the group that can do no wrong. They're just the group that never gets caught.
Hypothesis
I imagine a contingent of Turkers who have optimized their workflow to a tee. It's not easy to make a solid hourly wage from Turking, so one has to maximize productivity. Tasks below a certain financial payout or that take too long to do are not an option. HITs where quality can be ensured (identifying objects in images, transcribing audio) are only worthwhile if they pay well. HITs that can be easily gamed, however (multiple-choice surveys, coin-flips) are ripe for cheating - why not?
In an extreme state of the world, I imagine a cabal of Turkers somewhere, collaborating to maximize their effective hourly wage. Members would take turns looking at new tasks and figuring out (or even using software to measure) the expected hourly wage of a particular task. Other members in the group would then be sent links to the 'juiciest' tasks, and some sort of queue system would be used to manage what a particular cabal member's next task ought to be. Note: we're looking into whether we can trace any evidence of something like this and will post about them at a later point.
Why, then did this hyper-efficient cabal not invade our 2c/4c experiment? Quite simply, the 2 cents advertised (the other 2c came as a bonus) initially likely flew well below their radar as a task not worth any time at all. Instead, the 19 people who did come to us from the 100% group are more likely to be the 'part-timers' - people who answered Panos Ipeirotis' 'Why do you Turk' survey with either "it's fun" or "it's rewarding." This group is not financially motivated and less likely to cheat.
These altruistic Turkers are a minority, however; once money comes into play, they get Crowded In by the 100% optimizers.
Crowding In
In behavioral economics, crowding in is the idea that paying too much for a task may get the wrong kind of people to do it. A classic example of crowding in is paying for blood donations, outlawed in the US and most of the rest of the world for several decades now. The problem, as Richard Titmuss described in The Gift Relationship: From Human Blood to Social Policy, is that offering cash for blood gets the exact wrong kind of blood donor: the type that could really go for some cash right now and therefore may not have the cleanest blood available.
Similarly, as we offer increasingly larger enticements to participate in the coin flip experiment, we seem to be crowding the 'doing this for fun' crowd out in favor of the 'optimizer' crowd. The effect should be particularly evident in the 100% group, where both a lot of altruists and a lot of optimizers are likely to end up, altruists because they do good work and optimizers because it pays to be qualified for restrictive tasks.
Experiment
Luckily, this turned out to be a reasonably simple thing to test. Taking the 100%-ers as our experiment and 95-97% as our control group, we offered the same coin-flip experiment to 50 participants in each group and altering the payment for tails/heads to, one after the other, 10c/15c and 3c/8c. We kept the bonus at 5 cents and altering only the original offer, since the base payment is the only number Turkers can see before accepting the HIT.
Results
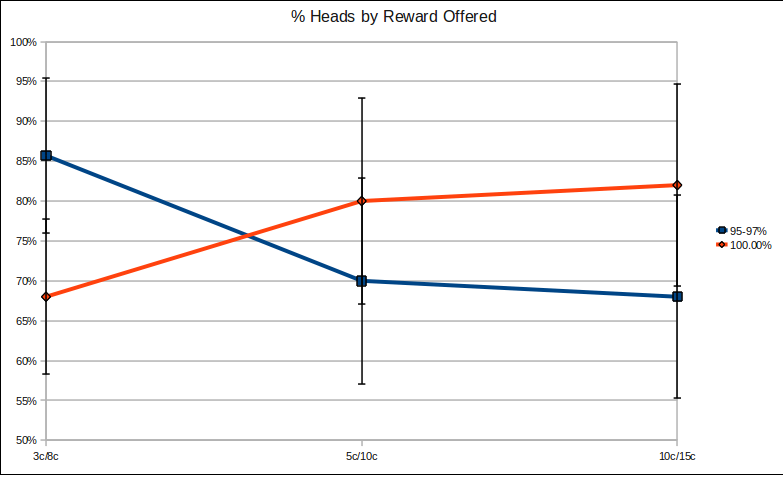Note: Error bars are at a 95% confidence interval.
From our experiment, it looks like while offering more money leads to more cheating for the 100% group, cheating actually goes down for the 95-97% control group. This fits with our hypothesis: in the 95-97% group, adding more money disincentives cheating - 5 cents for cheating looks less enticing if I've already received 10 cents and more enticing if I've only received 3. Dishonesty can be bought, but only at a reasonable multiplier to the base reward.
In the 100% group, however, the opposite occurs: the more money is offered, the more interesting the task becomes to optimizers, and optimizers cheat whenever they can get away with it.
The results are not quite statistically significant, as the error bars illustrate, but they tell a reasonably compelling story nonetheless.
Do you agree with our hypothesis? What other, alternate explanations might exist for these results?
Next Steps
We collected additional data about the Turkers as we conducted our experiment. Here's some of the analysis I intend for Part 3:
- Cheating by Time Taken: Can we predict whether a Turker really flipped a coin or not by looking at how long the assignment took them?
- Cabal Trends: Can we identify any collusion amongst Turkers? Assuming Turkers share tasks, are there any patterns of heads-heads-heads-heads... in our data within a fairly short time span?
- National Trends: Most Turkers (>90%, in our case) are either in the US or in India. Do Americans or Indians cheat more? Is either group more likely to be 100%-ers? Are Americans less likely to accept low-paying tasks? We started tracking IPs only by the time we ran the 3c/8c and 10c/15c groups, but even that subset of data points remain interesting.
Any ideas for other interesting analysis I should run?
Tags: #behavioral-economics